Sistemas de representación: Entra en una nueva dimensión.

Sí, hasta hace nada yo también pensaba que las proyecciones eran una cosa mucho más idílica, más de irte a la plaza del pueblo con tu sillita y una manta (que por la noche siempre refresca) a ver las películas mientras los chiquillos corretean, pero qué va. Esto es otra cosa. ¡Y vaya cosa! No te puedes fiar de las palabras. Sin embargo la geometría es bastante exacta y en ella sí puedes confiar. Te explico rápidamente:

El Sistema de representación es una manera ordenada de conocer las formas geométricas, ya sean bidimensionales o tridimensionales, en un plano que sí o sí es bidimensional.

Se le llama descriptivo, cuando se usan un conjunto de normas concretas para dibujar un objeto sobre un plano o proyección, y existen varios sistemas según cómo queramos proyectar dicho dibujo: Sistema cónico, diédrico, axonométrico o de planos acotados.

Todos estos sistemas que hemos mencionado arriba pueden clasificarse en dos grupos: Perspectivos y de medida.

• Sistemas Perspectivos son aquellos en los que la proyección no muestra las dimensiones del objeto en su verdadera magnitud (como el cónico o el axonométrico)
• Sistemas de medida son los sistemas en los que el objeto que se proyecta reproduce una imaggen del mismo con sus dimensiones en su verdadera magnitud (como el diédrico o el de planos acotados)

Lo fundamental de esto es que en base a estas proyecciones se pueden reconstruir las figuras en la otra dimensión. Esto puede sonar confuso, pero con un ejemplo es más fácil de entender: Si hacemos una figura en 2D en cualquiera de estos sistemas de representación, será posible reconstruirla en 3D sin problema (y viceversa).

El ejercicio que os traemos hoy para nutrir esas cabecitas sedientas de proyecciones propone hallar la Intersección (I) entre recta y plano en sistema diédrico. ¿Preparado? ¡Vamos allá!

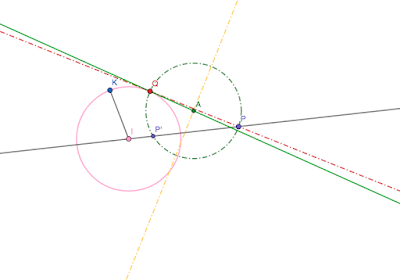
En este caso nos encontramos en el plano una recta (r) oblicua y un plano alfa (a) que también es oblicuo.

Lo primero que haremos será, puesto que ya tenemos alfa colocada en el plano, colocar la recta r en un plano beta (b). Para conseguir esto, beta2 debe pasar por v2 y beta1 por h1 (los puntos donde cortan ambos planos). No te preocupes si no entiendes de qué hablamos si estos aún no aparece en el dibujo que aparece arriba. Poco a poco.

Como alfa2 debe tener la misma inclinación que b2, simplemente alargaremos r2 hasta que corte con la linea de tierra. Beta1 (b1) es perpendicular al punto de tierra, para calcularlo haremos una recta perpendicular desde el punto donde b2 corta al punto de tierra y que acabamos de sacar. 

Ahora que ya tenemos tanto el plano alfa como el beta situados, procederemos a intersectarlos. Lo haremos así para obtener una nueva recta, a la que llamaremos S, y que más adelante veréis por qué es importante.

El punto donde cortan a2 y b2 será v2, y el punto donde corta a1 con b1 será h1. h2 es fácil de encontrar también, puesto que está en la línea de tierra. y v1 lo calcularemos trazando la perpendicular por v2 

Al conectar h2 con v2 y h1 con v1 obtendremos la recta S que veníamos buscando en sus dos proyecciones.

Para finalizar, interseccionaremos la recta r, que es la recta que nos han dado inicialmente, con la recta s, que es la que acabamos de dibujar. ¿Que por qué? Pues es muy sencillo: este punto de corte será la intersección que nos piden en el enunciado.

s2 y r2, como veis, son exactamente la misma recta. Esto nos dice que se cortan y se superponen a la vez en todos los puntos que la componen. s1 y r1 tienen su punto de intersección visible, así que lo marcamos como i1. El último paso que haremos será dibujar una perpendicular a la linea de tierra desde i1 que corte con las rectas s2 y r2 y marcaremos ese punto como i2.

Y ¡fin! Ya tenemos la intersección que corta la recta r con el plano alfa. ¡Practica en casa y déjame tus dudas en comentarios para que las resolvamos juntos!

Curvas Cónicas After Christmas Parte 2: La Parábola

 Seguimos con el apasionante mundo de las cónicas. Aunque hoy sea la noche de reyes, este post se lo dedicamos a la parábola y, por tanto, a sus principales elementos: recta tangente y circunferencia focal. Si no sabes de lo que te hablo, es que no has leído el post anterior sobre la elipsis, así que ¡ya estás tardando!

La definición que encontramos de parábola es que es una curva plana, de una rama abierta. Es el lugar geométrico de los puntos (P) que equidistan -marcado con línea discontinua en morado- del foco (un punto fijo llamado F) y de una recta fija a la que llamamos directriz (d).

 El eje de la parábola es la línea recta (en este caso la hemos pintado de rojo para que sea más fácil reconocerla) donde se sitúa el foco y es perpendicular a la directriz (d). También tiene un vértice (v), situado en el punto medio entre la directriz y el foco en este mismo eje.

 La razón de que esté dibujada desde el principio la recta perpendicular que va desde P a la directriz es que este punto resultante es F'', un punto que nos ayudará a encontrar fácilmente los elementos que interfieren en esta figura.

La recta tangente podemos obtenerla de la siguiente manera: Una vez tenemos F'', procedemos a trazar un segmento que lo una con F. A este segmento le hacemos la mediatriz, y esta será la recta tangente que buscamos.

Si seguimos con la dinámica de buscar la circunferencia focal, como ya hicimos con la anterior figura (que fue la elipsis, ¿de verdad aún no has ido a ver el post?), podemos volvernos locos, puesto que la definición que hemos visto de esta circunferencia no es válidad para la parábola, y lo que tendremos será una recta que coincide con la directriz. Esto también pasa con lo que sería la circunferencia principal, y también coincide con una recta, pero en este caso se trata de una recta tangente a la parábola en el vértice. 

 

Con estos truquis del almendruqui que acabo de dejar aquí, vamos a resolver juntas el siguiente problema:

Dada la recta tangente (t), un foco (F) y un punto (P), halla el punto de tangencia que esta recta t tiene sobre la parábola, su directriz y el eje.

Visto así puede parecer un poco caótico este dibujo de aquí arriba, pero con estos sencillos pasos tú también podrás dibujar la parábola que te mereces. Si queremos dibujar la directriz, lo primero que hay que saber es su definición: En una parábola, es el conjunto de simétricos del foco respecto a todas las rectas tangentes. Lo que haremos será dibujar el simétrico del foco F respecto a la recta t puesto que si hallamos F' estaremos un poquito más cerca de dibujarla, ya que cortará directamente con ella. 

El siguiente paso que vamos a dar para conseguir nuestra directriz es a través de P. 

Para que este punto pueda pertenecer a dicha parábola, os recuerdo que tiene que equidistar tanto de la directriz como de F, así que con radio PF, trazamos una circunferencia con centro en P. para, a continuación, dibujar la directriz*, que será la recta tangente de F' a la circunferencia que acabamos de realizar. Esto se hace uniendo P con F' y trazando la mediatriz tendremos el punto M y que marca la mitad del segmento. M es centro de una circunferencia que va a cortar a la anterior en el punto de tangencia que elijamos en cada caso.

*Aquí es interesante apuntar que existirían dos soluciones, puesto que la recta que trazamos desde F' al punto que corta con la circunferencia puede hacerse a ambos lados de esta.

Gracias a la directriz podemos a su vez dibujar el eje, realizando una recta perpendicular a dicha directriz que pase por F, tal que así:

 Después sólo nos quedaría saber dónde está el punto de tangencia sobre la recta t. Para esto hay que trazar una recta desde F' que sea, o bien paralela al eje, o paralela al radio de tangencia desde P hasta la X. Como ya tenemos el eje, le haremos su paralela desde F' hasta que corte a la recta tangente (t)

Parece mentira que esté terminado, ¿verdad? ¿quizás mejor así?:

 

Curvas Cónicas After Christmas Parte 1: La Elipse

 Sí, llegó diciembre y parecía que no volveríamos nunca a vernos las caras, pero terminó la Navidad y con ellas este letargo geométrico. Empezamos el año más fuertes que la nieve con las curvas cónicas.

Es cierto que hemos bautizado este post con el nombre de "Curvas Cónicas After Christmas" y todavía no han terminado. Pero seamos sinceros, ¿es que váis a hacer algo antes de que acaben realmente?

No me enrollo más. Por definición, estas curvas son las resultantes de las diferentes interseccionesentre un cono y un plano. Si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas.

Existen cuatro tipos: Elipse, Parábola, Hipérbola y Circunferencia.

 

Imagen del blog: https://dibujotecni.com/geometria-plana/curvas-conicas/

 

Hoy nos vamos a centrar en conocer y comprender el concepto de elipse y sus elementos principales, ya que nos abrirá muchas puertas de cara a ejercicios más avanzados.

 

La elipse es una curva plana y el lugar geométrico de unos puntos que, al sumar su distancia respecto de los focos (puntos fijos F y F'), el resultado es siempre constante e igual al eje mayor de esta elipse. Es decir, aquí b + c = 2a.

Los elementos que explicaremos a continuación conforman una elipse y son circunferencia principal, circunferencia focal y recta tangente. 

Si lo que queremos es hallar la circunferencia focal de la elipse que hemos dibujado arriba, lo que haremos será prolongar el segmento FP tomando la distandia F'P y poniéndola sobre dicho segmento, lo que nos dará el punto F''.

¿Todo esto, para qué? Bueno, pues es que la circunferencia focal será aquella que, con centro en uno de sus focos y con un radio 2a (el eje mayor de la elipse, marcado en narana en la figura de arriba). Gracias al paso anterior, vemos que ésta pasa por el punto que acabamos de hallar, F''.

F'' también nos servirá para obtener la recta tangente, ya que en este caso se construye uniendo en primer lugar F' con F''. A este segmento le hacemos la mediatriz, y esta será la recta tangente de la elipse que pasa por el punto P.

La circunferencia principal podemos dibujarla con centro en O y diámetro AB. Lo importante de esta circunferencia es que pasa por los puntos medios de todas las rectas tangentes a la elipse. En este caso mostramos cómo corta por el punto medio del segmento surgido al unir F' y F''.

 

 

Una vez tengamos claro estos tres conceptos nos será más fácil resolver problemas como este que os dejo a continuación:

Dada una elipsis definida por sus focos (F y F') y la tangente (t), hallar sus ejes y el punto de tangencia en la recta t 

Si hacemos un repaso de lo que acabamos de explicar, en seguida nos damos cuenta de que necesitamos F'' para poder resolver este problema, puesto que su mediatriz con F' es fundamental para conseguir el punto de tangencia. Lo más sencillo es realizar una recta perpendicular que corte a t. Esto nos dará un punto el cual debemos utilizar como centro de una circunferencia que nos mostrará dónde se encuentra F''

 

Con F'' ya podemos dibujar la circunferencia focal y estar un pasito más cerca de la victoria. ¿Que cómo se hace eso? Yo te lo digo: Cogiendo F'' como centro de esta circunferencia, teniendo como radio la distancia que hay hasta F. Este radio es CLAVE, porque tiene una longitud 2a y por lo tanto ya sabremos el eje mayor de la elipse que estamos buscando.

 

Si no te parece bastante el subidón que te estoy proporcionando dándote la medida del eje mayor, deja que termine de conquistarte con este dato: En el punto donde F'' corta a la recta tangente, ¡está el punto de tangencia! Le llamaremos P, para no perder las costumbres. Aquí un zoom de la figura anterior:

Ahora es el momento en que las mediatrices toman protagonismo. Una mediatriz la haremos entre el semento F'-F'' para conseguir el eje mayor que ya hemos mencionado (al punto medio lo llamamos M; la otra la haremos entre el segmento F-F', la necesitaremos para ubicar el eje menor y por tanto el centro de la elipse, al que llamaremos O.
 

 

No hay tiempo para tonterías, ¡hay una elipsis que dibujar! Tenemos la medida de nuestro eje mayor y vamos a proceder a marcarla. Para ello cogemos la medida del segmento MF y lo transportamos al centro de la elipse, que en nuestro caso se llama O, y ya tendremos las medidas del eje. 

Esto está prácticamente hecho: Tenemos el eje mayor, el punto de tangencia de la recta t y nos quedaría simplemente el eje menor, del cual sabemos en qué dirección va a estar y que sus extremos van a estar a una distancia de los focos igual a medio eje mayor (es decir, cogemos de radio la distandia OB, por ejemplo, y con centro en F y F' vamos haciendo las circunferencias. Donde converjan se encontrarán los puntos C y D).

Glosario for dummies

Tiempos desesperados exigen medidas desesperadas, y ante la avalancha de tecnicismos constantes que van apareciendo entre nuestros problemas, hemos decidido crear esta entrada, que se irá actualizando en función de los conceptos que estudiemos o las dudas surgidas.

Están por orden alfabético, ¡así te será más sencillo encontrar el término que buscas!

Antiparalelismo: En geometría, un par de rectas concurrentes son antiparalelas una de la otra respecto a otro par de rectas si la bisectriz del ángulo que forma el primer par es perpendicular a la bisectriz del ángulo formado por las otras dos. La propiedad de antiparalelismo es simétrica: si un par de rectas son antiparalelas respecto al segundo par, entonces el segundo par es antiparalelo respecto al primero.

Arco capaz: El arco capaz es el lugar geométrico de los puntos desde los que un segmento AB se «ve» con el mismo ángulo, es decir, el lugar geométrico de los vértices P de los ángulos APB que tienen la misma amplitud.

Asíntota: Una recta que, a medida que se prolonga de manera indefinida, tiende a acercarse a una cierta curva o función, aunque sin alcanzar a hallarla.

Bisectriz: Es la semirrecta con origen en el vértice del ángulo y que lo divide en dos ángulos de igual medida.​ Es una recta si se considera como el lugar geométrico de los puntos del plano que equidistan, es decir, están a la misma distancia de los lados del ángulo bisecado.

Eje: Una línea imaginaria alrededor de la cual algo rota. 

Elipse: La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos, llamados focos, es constante.

Geometría proyectiva: Es la rama de la matemática que estudia las propiedades de incidencia de las figuras geométricas, pero abstrayéndose totalmente del concepto de medida. A menudo se usa esta palabra también para hablar de la teoría de la proyección llamada geometría descriptiva*.

Geometría descriptiva*: Es un conjunto de técnicas geométricas que permite representar el espacio tridimensional sobre una superficie bidimensional. Por tanto, mediante una «lectura» adecuada posibilita resolver problemas espaciales en dos dimensiones de modo que se garantiza la reversibilidad del proceso.

Hipérbola: Es una curva abierta de dos ramas, obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.

Intersección: En geometría, una intersección es un punto, línea recta, curva, superficie o volumen, que es común a dos o más elementos. El caso más simple en geometría euclidiana es la intersección de dos rectas distintas, que o bien es un punto o no existe si las líneas son paralelas.

Inversión: En geometría se denomina inversión a una aplicación que establece una correspondencia biunívoca entre los puntos del exterior y los puntos del interior de una circunferencia dada en un plano. Se dice que dos puntos P y P ′ guardan una relación de inversión con respecto a la circunferencia ( C )  de centro O y radio R, cuando se cumple que:

    1.Los puntos P ′ y P están sobre una misma semirecta con origen en O
    2.Sus distancias cumplen la igualdad

Mediatriz:La mediatriz de un segmento es la línea recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geométrico — la recta — cuyos puntos son equidistantes a los extremos del segmento.

Parábola: En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.

Perpendicularidad: se da entre dos entes geométricos que se cortan formando un ángulo recto. 

Perspectiva axonométrica: es un sistema de representación gráfica consistente en representar elementos geométricos o volúmenes en un plano mediante proyección ortogonal u oblicua referida a tres ejes ortogonales, de tal forma que conserven sus proporciones en cada una de las tres direcciones del espacio: altura, anchura y longitud.

Perspectiva caballera: Es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.

Plano: Es un objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas; es un concepto fundamental de la geometría junto con el punto y la recta.

Potencia: En geometría la expresión potencia de un punto respecto una circunferencia se refiere al valor constante que resulta de multiplicar las longitudes de dos segmentos definidos en una misma recta que pasa por dicho punto y es secante o tangente a dicha circunferencia.

Problema de Apolonio: En geometría plana euclidiana, el problema de Apolonio consiste en encontrar las circunferencias tangentes a tres circunferencias dadas. Apolonio de Perge propuso y resolvió este problema en la obra Ἐπαφαί, .

Proyección isométrica: es un método de representación gráfica, más específicamente una axonométrica​  cilíndrica ​ortogonal.​ Constituye en una representación visual de un objeto tridimensional que se reduce en dos dimensiones, en la que los tres ejes ortogonales principales, al proyectarse, forman ángulos de 120°, y las dimensiones paralelas a dichos ejes se miden en una misma escala.

Sección cónica: Se denomina sección cónica a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

Segmento: Es la parte de la recta que esta delimitada por dos puntos que son los extremos del segmento, por tanto se puede medir su longitud. 

Simetría: La propiedad de un objeto o figura cuando las características (forma, tamaño y posición relativa de sus partes) son las mismas en ambos lados de una línea divisora o en torno a un centro.

Sistema Americano y Europeo: En el Sistema Americano el plano de proyección se coloca delante del objeto en el sentido de la proyección. En el sistema europeo el plano se coloca detrás del objeto en el sentido de la proyección.

Tangente: La tangente ​ a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo con la curva en la vecindad de dicho punto.

Determinación del inverso de un punto. Estudio de construcciones

Dada una inversión definida por su centro (I) y la potencia (K que es el radio de la circunferencia de auto-inversión), determinar el inverso de un punto mediante al menos tres construcciones diferentes. 

Vamos a empezar por las definiciones de los términos que aparecen en este enunciado para que no te pierdas en ningún momento:

En geometría se denomina inversión a una aplicación que establece una correspondencia biunívoca entre los puntos del exterior y los puntos del interior de una circunferencia dada en un plano, de forma que:

Se dice que dos puntos y guardan una relación de inversión con respecto a la circunferencia de centro y radio , cuando se cumple que:

Los puntos y están sobre una misma semirecta con origen en .

Sus distancias cumplen la igualdad: 

Sabiendo esto, veamos tres maneras distintas de obtener P':

1. Determinación del inverso de un punto mediante el teorema del cateto:

Este teorema funciona mediante medias proporcionales de los catetos con sus proyecciones sobre la hipotenusa y el producto que resulta. Sabiendo esto:

-Trazaremos una recta que pase por I y por P, ya que el inverso de P siempre estará en algún lugar de esa recta. 

- El siguiente paso es dibujar el triángulo rectángulo en el que basaremos nuestra estrategia de obtención de P':

*ES MUY IMPORTANTE SABER QUE HALLAMOS EL PUNTO Q PARA QUE SU INVERSO ESTÉ EN EL MISMO SITIO (¡¡todos los puntos que están en esta circunferencia son dobles!!) Y QUE Q=Q' EN ESTOS TRES EJERCICIOS ANTES DE CONTINUAR*

- Con esto, lo que sabemos es que: Segmento IQ es un cateto (y el radio de la circunferencia de inversión) al igual que el segmento QP, y la hipotenusa la forman IP.

Lo  que necesitamos para completar el ejercicio es sacar la proyección del cateto IQ (o de K, que viene a ser lo mismo)

La fórmula del teorema del cateto que queremos utilizar es la siguiente:

cateto (IQ) al cuadrado es igual a la hipotenusa (IP) por la proyección del cateto sobre la hipotenusa.

Por lo tanto, en el punto que la proyección corte al segmento IP, obtendremos P'.

2. Determinación del inverso de un punto mediante el teorema de la altura:

- Volvemos a nuestra posición inicial:

- Y también volvemos a dibujar nuestro triángulo rectángulo:

El teorema de Tales nos dice que "Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado", por lo que, efectivamente, trazamos una paralela, y lo será al cateto QP:

¿Que por qué la paralela pasa por ahí? Pues bien, la información que tenemos es que P' siempre estará en la recta que forman I y P, por lo que la paralela a QP que acabamos de trazar tendrá que dibujarse a partir del
punto que corta la recta IP y coincide con la circunferencia de autoinversión.

Y así, el punto de esta pequeña circunferencia que acabamos de hacer que corta con el segmento IP nos habrá dado la posición de P' y ¡problema resuelto!

3. Determinación del inverso de un punto mediante potencias:

Aquí estamos de nuevo. ¿Y ahora qué?

Repasando lo anterior, Q y Q' estarán en el mismo sitio, ya que pertenecen a la circunferencia de inversión, y P' estará en la recta que trazamos desde I a P.

Para encontrar dónde se encuentra P' nuestra misión es hacer la circunferencia que pase por P y por Q, y el punto donde corte la recta IP será el resultado. ¡Vamos a ello!

-Elegimos un punto Q (Q=Q') y procedemos a hallar la circunferencia que corta por esos dos puntos. Esto se hace dibujando una recta que pasa por P y Q y trazando su mediatriz, ya que el centro de la circunferencia estará en ella:

- Para encontrar P' tenemos que saber que el centro de la circunferencia que vamos a proceder a trazar ha de ser tangente a la circunferencia primigenia (la de autoinversión) pasando el punto Q' (que viene a ser lo mismo que Q, ya sabéis, pero por si acaso lo voy recordando) y cortando con la mediatriz que acabamos de hacer. A este centro lo hemos llamado A.

- Habiendo encontrado el punto A, trazamos una circunferencia que pasa por P y Q y en el punto donde corta con la recta IP, ¡Voilá! ya tenemos P'.