Determinación del inverso de un punto. Estudio de construcciones

Dada una inversión definida por su centro (I) y la potencia (K que es el radio de la circunferencia de auto-inversión), determinar el inverso de un punto mediante al menos tres construcciones diferentes. 

Vamos a empezar por las definiciones de los términos que aparecen en este enunciado para que no te pierdas en ningún momento:

En geometría se denomina inversión a una aplicación que establece una correspondencia biunívoca entre los puntos del exterior y los puntos del interior de una circunferencia dada en un plano, de forma que:

Se dice que dos puntos y guardan una relación de inversión con respecto a la circunferencia de centro y radio , cuando se cumple que:

Los puntos y están sobre una misma semirecta con origen en .

Sus distancias cumplen la igualdad: 

Sabiendo esto, veamos tres maneras distintas de obtener P':

1. Determinación del inverso de un punto mediante el teorema del cateto:

Este teorema funciona mediante medias proporcionales de los catetos con sus proyecciones sobre la hipotenusa y el producto que resulta. Sabiendo esto:

-Trazaremos una recta que pase por I y por P, ya que el inverso de P siempre estará en algún lugar de esa recta. 

- El siguiente paso es dibujar el triángulo rectángulo en el que basaremos nuestra estrategia de obtención de P':

*ES MUY IMPORTANTE SABER QUE HALLAMOS EL PUNTO Q PARA QUE SU INVERSO ESTÉ EN EL MISMO SITIO (¡¡todos los puntos que están en esta circunferencia son dobles!!) Y QUE Q=Q' EN ESTOS TRES EJERCICIOS ANTES DE CONTINUAR*

- Con esto, lo que sabemos es que: Segmento IQ es un cateto (y el radio de la circunferencia de inversión) al igual que el segmento QP, y la hipotenusa la forman IP.

Lo  que necesitamos para completar el ejercicio es sacar la proyección del cateto IQ (o de K, que viene a ser lo mismo)

La fórmula del teorema del cateto que queremos utilizar es la siguiente:

cateto (IQ) al cuadrado es igual a la hipotenusa (IP) por la proyección del cateto sobre la hipotenusa.

Por lo tanto, en el punto que la proyección corte al segmento IP, obtendremos P'.

2. Determinación del inverso de un punto mediante el teorema de la altura:

- Volvemos a nuestra posición inicial:

- Y también volvemos a dibujar nuestro triángulo rectángulo:

El teorema de Tales nos dice que "Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado", por lo que, efectivamente, trazamos una paralela, y lo será al cateto QP:

¿Que por qué la paralela pasa por ahí? Pues bien, la información que tenemos es que P' siempre estará en la recta que forman I y P, por lo que la paralela a QP que acabamos de trazar tendrá que dibujarse a partir del
punto que corta la recta IP y coincide con la circunferencia de autoinversión.

Y así, el punto de esta pequeña circunferencia que acabamos de hacer que corta con el segmento IP nos habrá dado la posición de P' y ¡problema resuelto!

3. Determinación del inverso de un punto mediante potencias:

Aquí estamos de nuevo. ¿Y ahora qué?

Repasando lo anterior, Q y Q' estarán en el mismo sitio, ya que pertenecen a la circunferencia de inversión, y P' estará en la recta que trazamos desde I a P.

Para encontrar dónde se encuentra P' nuestra misión es hacer la circunferencia que pase por P y por Q, y el punto donde corte la recta IP será el resultado. ¡Vamos a ello!

-Elegimos un punto Q (Q=Q') y procedemos a hallar la circunferencia que corta por esos dos puntos. Esto se hace dibujando una recta que pasa por P y Q y trazando su mediatriz, ya que el centro de la circunferencia estará en ella:

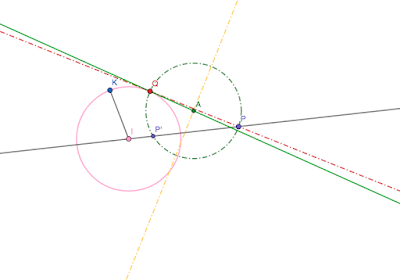
- Para encontrar P' tenemos que saber que el centro de la circunferencia que vamos a proceder a trazar ha de ser tangente a la circunferencia primigenia (la de autoinversión) pasando el punto Q' (que viene a ser lo mismo que Q, ya sabéis, pero por si acaso lo voy recordando) y cortando con la mediatriz que acabamos de hacer. A este centro lo hemos llamado A.

- Habiendo encontrado el punto A, trazamos una circunferencia que pasa por P y Q y en el punto donde corta con la recta IP, ¡Voilá! ya tenemos P'.